A thought experiment concerning back radiation
A common illustration of the greenhouse effect is the idealized greenhouse model. This model captures some important features of the earth as a system in radiative balance. This figure from the Wikipedia page shows the basic idea.

To solve the system in equilibrium, we can use the Stephan-Boltzmann law $$j=\sigma T^4$$ on each of the layers, modified by a non-unity emissivity $$\varepsilon$$ for the atmosphere. Incoming solar and outgoing radiation have very little overlap in their spectra, so to an ok approximation, we can treat them as non-overlapping.
In this equilibrium system there are two opposite fluxes of longwave radiation energy, from the earth up and from the atmosphere down (the back radiation). This makes the net flux of energy away from the surface lower than it would have been at a given tempereature in the absence of the atmosphere, making the surface of the earth warmer to compensate.
Some context
Why is this important? In a lot of places on the internet, there are all sorts of discussions concerning the nature and existence of this back radiation, usually in the context of the second law of thermodynamics making the flux of energy from the atmosphere to the surface impossibl, or forbidding it heating the surface. See this series of posts at The Science of Doom for a thorough discussion.
Another discussion is about the physical existence of the back radiation as a separate flux of energy, or whether the prescence of the atmospheric emission of electromagnetic energy simply modulates the instantaneous radiation field leading to the net flux of upward energy. I have only recently come across this discussion in the comments at Terje Wahl’s blogg (in norwegian). This started me thinking, and I spend a good part of the previous weekend starting to devise a thought experiment to try to argue for the physical existence of this energy flux.
Conventional physics, as I was taught it in non-climate related thermodynamics, considers the back radiation to be real, but I like thinking about this kinds of thing.
In the following I’ll use the conventional definitions of shortwave and longwave radiation as $$\lambda < 4 , \mu m$$ and $$\lambda > 4 , \mu m$$ respectively
The thought experiment
At $$z=0$$ we place a perfectly absorbing and emitting infinite plate (i). Homogeneous monochromatic ultraviolet radtiation ($$\lambda=200, nm$$) is coming from an energy source at infinite distance from our setup, and radiating towards the plate at $$z=0$$. At some finite distance $$z$$, far from (i) is another plate (ii), perfectly transmitting for the incoming UV radiation and with constant absorptivity $$0 < \alpha < 1$$ for all wavelengths except $$\lambda=200, nm$$. Both plates are thin, perfectly conducting and with negligible heat capacity. Right underneath plate (i) is a layer with emissivity 0, so that no energy is lost in that direction. Between the plates, and outside the setup is perfect vacuum.
The distance between the two plates is large. So large that the transit time for radiation between them is much larger than the time it takes each plate to equilibrate with the incoming energy.
At time $$t=0$$ the system is in equilibrium, with incoming radiation balanced by thermal radiation from (i) and (ii). At time $$t=t_1$$ the absorptivity of (ii) is changed, to become closer to 1. As a consequence, the plate will quickly equilibrate to a new temperature and a new thermally radiating state. This change in the state of (ii) will not be detected by (i) for some time, since the information travels with the speed of light. At a later time $$t=t_2$$ the information reaches (i) which then equilibrates with the new state of (ii). This will then lead to a series of temporally distinct equilibrations to the new state in a feedback, until a new internal state of the system is realized in equilibrium with the incident radiation. This new internal state will contain a larger amount of energy.
An illustrative simulation of the time evolution of this system is shown in the figures below. The simulation code can be found here
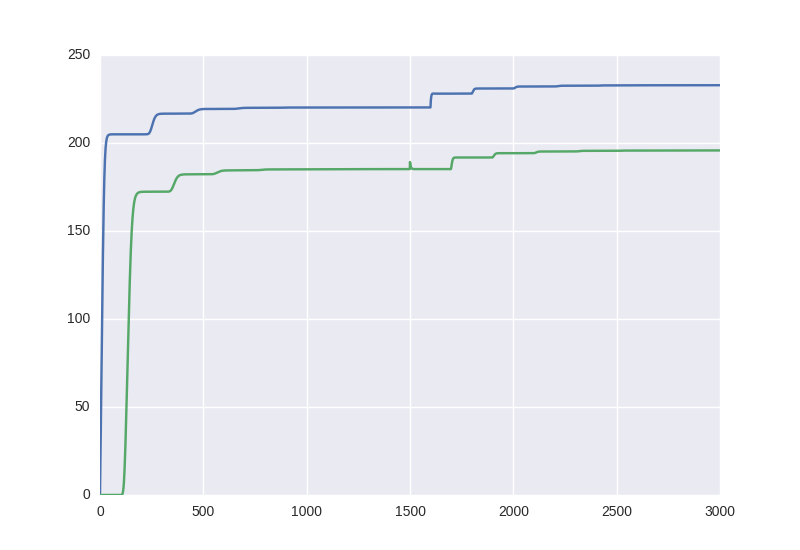
Figure 1: Temperature evolution of the system described above.
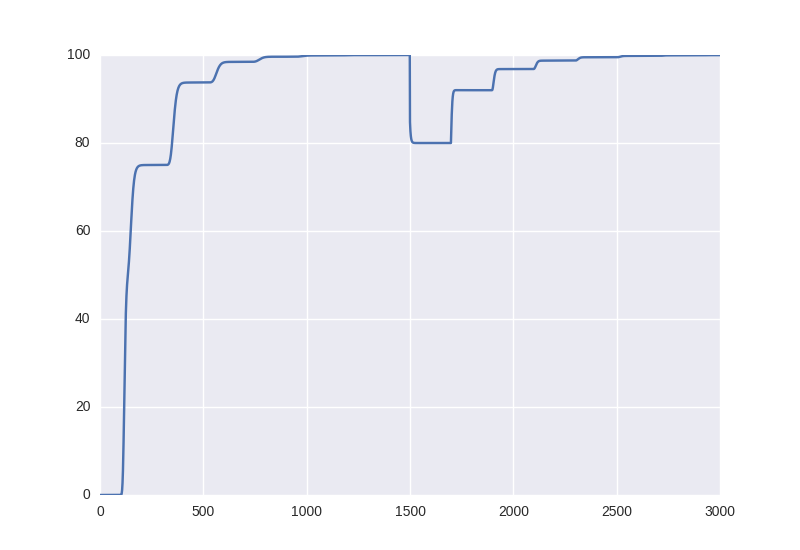
Figure 2: Outgoing radiation outside plate (ii). In equilibrium, this is equal incoming energy.
What does this thought experiment tell us about the physical nature of the net transfer of energy from the surace to the greenhouse layer? The net transfer of energy happens between two plates that are isolated from knowing about the state change of the other for a long time, the information about this change will travel with the speed of light, and an instantaneous modulation of the net radiation field by this information is not a plausible explanation. In my opinion, the only reasonable way to describe the energy flow in this system is in terms of two energy fluxes leading to a net flux of energy aay from the surface.
When the transfer of radiation in the system can be considered instantaneous, the two views on the nature of the energy flux are equivalent. But the assumption of instantaneous transfer is only an approximation, so the same argument applies in principle in the normal idealized greenhouse model, as well as in the real atmosphere.